Python Dictionary는 어떻게 구현되었을까?
딕셔너리는 파이썬 프로그래밍에서 자주 사용되는 자료구조로, key-value pair 구조로 이루어져 있다.
그 구조는 마치 자바의 HashMap이나 Javascript의 JSON과 비슷한데, 그렇다면 저레벨 수준에서 구현은 어떠할까?
기본적으로 dict 타입은 저레벨 구현까지 내려가보면 해시 테이블로 구현되어 있다. 해시 테이블은 (Key, Value)로 데이터를 저장하는 자료구조 중 하나로 빠르게 데이터를 검색할 수 있는 자료구조이다. 해시 테이블이 빠른 검색속도를 제공하는 이유는 내부적으로 배열(버킷)을 사용하여 데이터를 저장하기 때문이다. 해시 테이블은 각각의 Key값에 해시 함수를 적용해 배열의 고유한 index를 생성하고, 이 index를 활용해 값을 저장하거나 검색하게 된다. 여기서 실제 값이 저장되는 장소를 버킷 또는 슬롯이라고 한다.
CPython에서 dictionary를 위한 해시테이블의 각 원소는 3가지 데이터로 이루어져 있다. 이 3가지 값들은 각각 hash, key, 그리고 value이다. 우선 key, value는 dictionary의 key와 value이며, hash는 key를 해시 함수에 적용한 값이다.
이 해시 테이블은 각 hash 값에 대해서 미리 정해진 mask로 마스킹을 한 값을 index로 사용한다. 즉, 해시 테이블은 고유한 n개의 hash 값에 대응하는 n개의 원소로 이루어진 배열이며, 각 원소는 대응하는 hash 값과 딕셔너리의 key와 value를 포함하는 구조로 이루어지게 된다.
해시 함수란 무엇인가?
해시 함수 (hash function) 또는 해시 알고리즘 (hash algorithm) 또는 해시 함수 알고리즘 (hash algorithm)은 임의의 길이의 데이터를 고정된 길이의 데이터로 매핑하는 함수 이다. 해시 함수에 의해 얻어지는 값은 해시 값, 해시 코드, 해시 체크섬 또는 간단하게 해시 라고 한다. 그 용도 중 하나는 해시 테이블 이라는 자료구조에 사용되며, 매우 빠른 데이터 검색을 위한 컴퓨터 소프트웨어에 널리 사용된다. 해시 함수는 큰 파일에서 중복되는 레코드를 찾을 수 있기 때문에 데이터베이스 검색이나 테이블 검색의 속도를 가속할 수 있다.
앞서 언급한 것과 같이, 해시 함수는 임의의 길이의 데이터에 대해서 `"고정된" 크기의 값으로 매핑하는 함수`를 말한다. 고정된 길이의 문자열들만으로 이 세상에 존재하는 모든 문자열, 숫자 등의 데이터들을 1:1 매핑하는 것은 불가능하다. 다시 말해, 서로 다른 데이터에 대해서 동일한 해시 값을 가지도록 만드는 경우가 언제든지 발생할 수 있다는 것이다. 일반적으로, 이러한 상황에 대해서 `해시 충돌(hash collision)`이라고 부른다.
위에서 나왔던 것처럼 해시 테이블은 해시 값을 키로 사용한다. 그렇다는 것은 사용자가 넣은 서로 다른 데이터들에 대해서 동일한 해시 값을 가지는 경우가 발생하는 경우에 대해서 대비를 해야 한다는 것이다.
해시 테이블에서 해시 충돌에 대응하는 방법
일반적으로 해시 테이블에서 해시 충돌에 대응하기 위한 알고리즘으로는 `체이닝(chaining) 알고리즘`과 `오픈 어드레싱 (Open Addressing) 알고리즘`이 있다.
우선, 체이닝 알고리즘은 동일한 해시 값을 가지는 데이터들을 Linked List나 Tree 등의 자료구조를 사용해서 모두 저장하는 방식이다. 충돌되는 모든 값들을 자료구조를 활용해서 저장함으로써 문제를 해결하는 방식이다.
이 방식의 가장 큰 문제점으로는 탐색 및 데이터 추가 등의 작업에 요구되는 시간 복잡도가 증가하게 된다는 점이다. Hash Collision이 자주 발생되면 단일 해시 키에 대해서 크기가 큰 Linked List 및 Tree가 생성되게 되고, 주어진 key에 대해서 대응하는 value를 검색하는 데이터 탐색 등의 복잡도가 최악의 경우 O(n)이 된다.

이와 대조되는 방법이 바로 Open Addressing 알고리즘이다. Open Addressing 알고리즘은 해시 값에 대응하는 버킷이 이미 다른 데이터에 의해 선점되었을 경우, 정확히 해시 키와 대응하는 index를 사용하는 것을 포기하고 Probing 작업을 통해 다른 빈칸을 찾아서 데이터를 저장한다. 이러한 Probing 작업에도 여러 종류가 존재하는데, 가장 단순한 알고리즘으로는 `Linear Probing`이 존재한다.
Linear Probing은 매우 직관적인데, 현재 index를 시작점으로 해서 모든 인덱스를 한칸씩 옮겨가면서 가장 먼저 만나는 빈칸을 타겟 index로 잡고 이에 대응하는 버킷에 데이터를 저장한다. 어떤 의미에서는 선형적으로 가장 가까운 포인트에 데이터를 저장한다는 장점을 가질 수 있겠지만, 해시 충돌이 날 때마다 O(n) 복잡도의 알고리즘을 수행해야 하며, 이렇게 다른 index에 저장된 데이터가 자주 접근되는 HotKey에 해당할 경우에는 시스템 전체의 성능이 크게 저하될 가능성이 높아지게 된다.
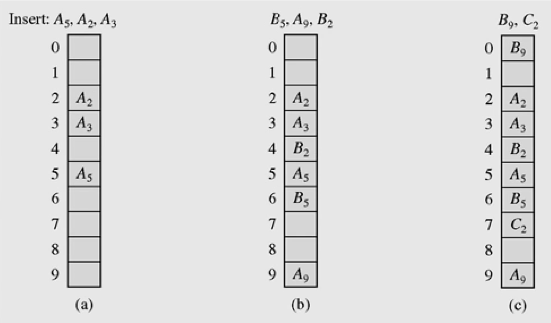
파이썬에서는 해시 충돌을 위해서 Open Addressing 알고리즘을 사용하고 있다. 그러나 Probing을 위해서는 Linear Probing이 아닌 `Perturbation Shift Probing`이라는 고유의 알고리즘을 사용하고 있다.
https://svn.python.org/projects/python/trunk/Objects/dictobject.c를 보면, 이 Probing에 대한 아주 긴 주석을 볼 수 있게 되는데, 이를 읽어보면 파이썬 언어 개발에 참여한 개발자들이 얼마나 많이 고민을 했는지에 대해서 알 수 있다.
기본적으로, 파이썬에서는 원래 사용하려 했던 인덱스 i가 사용 못하게 되었을 때 다음 후보 인덱스 j를 `mod 연산자(%, 나눗셈의 나머지)`를 응용한 수식을 사용해서 구하려고 한다.
j = i
j = (5*j) + 1
만약 `i = 1`이라면 다음과 같은 순서로 Probing 작업이 실행되게 된다.
1 -> 6 -> 7 -> 4 -> 5 -> 2 -> 3 -> 0 -> 1 …
바로 위의 수열만 보더라도 알 수 있듯이 이 알고리즘은 Probing을 진행하다보면 결국 시작점으로 되돌아오게 된다. 이러한 recurrence를 없애기 위해서 파이썬 개발자들은 새로운 변수를 추가하여 문제를 해결하게 된다.
initialize perturb with i
j = (5*j) + 1 + perturb;
perturb >>= PERTURB_SHIFT;
Use j % 2**i as the next table index
위의 알고리즘에서 볼 수 있듯이, 매 probing 차례마다 PERTURB_SHIFT라는 값만큼 비트 이동을 하는 변수 pertrub를 기존 인덱스 계산식에 추가함으로써 조금 더 다이나믹하게 Probing을 진행할 수 있도록 디자인하였다.
CPython 코드에서는 PERTURB_SHIFT는 5로 정의하였으나, 소스 코드 상의 주석에 따르면 필요에 따라 다른 값을 적용해서 성능을 튜닝할 수 있다고 한다. (물론, 왠만한 경우에는 파이썬 자체를 다시 컴파일 하는 경우가 없을테니 몰라도 무방한 내용이지 않을까 생각이 들기는 한다)
이러한 Open Addressing 알고리즘은 Chaining과는 다른 단점이 두 가지 존재한다. 우선, Open Addressing 알고리즘을 기반으로 하는 해시 테이블의 경우 이미 할당된 길이 이상의 index를 가질 수 없기 때문에 저장할 수 있는 데이터의 개수에 근본적으로 한계가 존재한다.
또한, Open Addressing 알고리즘 기반 해시 테이블의 경우 일정 수준 이상으로 테이블이 차게 되면 성능이 급격히 저하되는 문제가 발생하게 된다. 이는 일정 수준 이상으로 테이블이 차게 되면 해시 충돌이 발생하게 될 가능성이 크게 증가하면서 최악의 경우에는 Probing 알고리즘이 데이터 추가 시마다 작동되는 상황이 발생할 수 있기 때문이다.
이러한 이유로 인해, Open Addressing 기반 해시 테이블들의 경우 일정 수준 이상으로 데이터가 차게 되면 더 긴 배열로 이루어진 (더 많은 인덱스를 가지는) 해시 테이블을 새로 생성한 뒤, 기존 데이터들을 모두 새로 생성된 해시 테이블로 옮기는 작업을 가지게 된다. 파이썬에서는 이 "일정 수준"을 해시 테이블 사이즈의 2/3 (66%) 이상이 차는 경우로 정의하고 있다. 참고로 루비에서는 이 값을 1/2, 즉 50%로 정의하고 있다.
해시 테이블의 크기는 어느 정도일까?
우선, 파이썬 딕셔너리를 위한 해시 테이블의 초기 크기는 PyDict_MINSIZE (소스코드에 의하면 이 값은 8로 정의되어 있다)이며, 크기를 키울 때마다 현재 크기의 4배씩 크기를 키우며, 크기가 일정 수준 이상으로 너무 커지게 되면 (소스 코드 상으로는 50,000 이상일 경우에) 더 큰 테이블을 만들 때 2배씩 크기를 키우게 된다.
이렇게 2~4배씩 크기를 키우는 이유에 대해서 파이썬 개발자들은 "딕셔너리의 희소도(sparsity)가 높아야 성능이 더 안정적이기 때문에 한번 크기를 키울 때 일정 수준 이상으로 키우는 것이 성능 향상에 더 도움이 된다"고 주석에 써 놓았다.
참고자료
https://svn.python.org/projects/python/trunk/Include/dictobject.h
https://svn.python.org/projects/python/trunk/Objects/dictobject.c
'Python' 카테고리의 다른 글
| pip-audit과 GitHub Actions를 활용한 취약 라이브러리 탐지 파이프라인 구축하기 (0) | 2023.10.09 |
|---|---|
| 소스코드 레벨에서 비교하는 Python List와 Set의 차이 (2) | 2023.10.09 |
| gunicorn과 nginx를 사용해서 Flask 앱 배포하기 (0) | 2023.10.09 |
| flask - "ImportError: cannot import name ‘parse_rule’ from ‘werkzeug.routing’" 해결법 (0) | 2022.10.01 |
| 파이썬에서 파일 크기 알아내기 (0) | 2022.09.14 |